Dato il titolo, questo potrebbe essere un articolo pasquale, ma non resisto, devo pubblicarlo ora.
I motivi sono i seguenti: L’argomento tra poco sarà di stretta attualità e ho appena sentito un tentativo di divulgazione del concetto da parte di una giornalista economica alla radio che si è aggrovigliata in un vortice di dati, lapsus ed affermazioni inesatte, che ne hanno reso totalmente incomprensibile la spiegazione. Spero di fare meglio!
La domanda è la seguente: perché il prezzo di obbligazioni e titoli di stato si muove? Perché può salire o scendere? Come è possibile, visto che a una certa data (la scadenza), se tutto va bene, coloro che hanno avuto in prestito i miei soldi me li restituiscono tali e quali?
Risponderò con un esempio (un apologo?) che utilizzo spesso e che mi serve per far capire la relazione tra prezzo delle obbligazioni, tasso delle cedole e tasso effettivo, ovvero quello riscosso dal risparmiatore.
Inizia il dramma…
Immaginate di essere un contadino e possedere una gallina che fa 1 uovo d’oro all’anno.
Tutti i sabati andate al mercato a sentire quanto vi pagherebbero la gallina dalle uova d’oro. La gallina vale più o meno 100 soldi, vi dicono.
Si sparge la voce che voi siete l’unico possessore di una gallina dalle uova d’oro e che una volta all’anno vi gratifica del suo prezioso dono.
Il sabato successivo al mercato trovate una schiera di compratori che offrono 110, poi 120, poi 130 soldi. Voi tenete duro. Niente da fare.
Dopo altri 7 giorni tornate al mercato e vedete un capannello di gente entusiasta intorno ad un tizio che tiene in mano una gallina e 2 uova d’oro ancora calde!
Così chiedete, un po’ inquieti, quanto vale ora la vostra gallina che fa 1 uovo d’oro all’anno. Vi risponde un tizio che un po’ schifato vi dice: “Al massimo posso darti 50 soldi!”
Così decidete di tenervi la gallina, finché la natura non farà il suo corso oppure qualcuno non vi darà 100 soldi precisi.
Bella storia, vero?
Bene! Se sostituiamo al termine Uova il termine Cedola e al termine gallina il termine (che sò) BTP, abbiamo una percezione abbastanza esatta di ciò che succede tutti i giorni sul mercato obbligazionario mondiale.
L’investitore, ad esempio, acquista all’emissione un titolo durata 10 anni con cedola 2% annua e lo paga 100. Dopodiché i tassi di mercato scendono e un titolo di uguale durata decennale l’anno successivo viene emesso dallo Stato con cedola 1%. Immediatamente il prezzo del primo BTP aumenta. Quanto?
Più o meno fino al corrispondente del rendimento del secondo titolo (considerato l’anno di meno di durata residua), quindi a spanne 108? 109? Il mercato, così, si incarica di rendere, per chi volesse, indifferente l’acquisto del primo o del secondo titolo.
Se un nuovo investitore dovesse scegliere tra il primo titolo e il secondo infatti, capirebbe che a scadenza avrebbe più o meno lo stesso rendimento, vicino all’ 1%.
Se però il contadino, pardon, l’investitore di prima vendesse dopo 1 anno di detenzione il titolo al 2% sul mercato, ricaverebbe un rendimento (in gergo “plusvalenza”) dell’8/9%, avendo comprato a 100 e rivenduto a 108/109.
In molti casi, per durate molto lunghe, negli ultimi anni i BTP hanno toccato anche quotazioni di oltre 150!
Mettiamo che l’investitore resista alla tentazione o sia semplicemente distratto.
Poniamo però che, dopo qualche anno, i tassi di mercato siano saliti al 4%. Quindi i titoli emessi in questo periodo avranno cedola 4%. Questo può accadere, ad esempio perché nel frattempo è aumentata l’inflazione e i tassi le sono andati dietro.
Il vecchio titolo, che produce il 2%, perderebbe di prezzo. Chi vuole un titolo che dà il 2% quando posso trovarne uno che da il 4%? Quanto perderebbe? Dipende in primo luogo dalla durata residua (per i più sofisticati, dalla “Duration“) però è possibile, anzi probabile, che scenderebbe ad un prezzo inferiore a 100, corrispondente più o meno, per chi lo acquistasse in quel momento, ad un rendimento ( a scadenza) del 4% annuo. Ad un prezzo di 90 ad esempio, l’acquirente dell’epoca avrebbe una plusvalenza di 10 (100 alla scadenza -90 prezzo acquisto) oltre alle cedole del 2% che riscuote fino alla scadenza. Se questa è dopo 5 anni, avrebbe ottenuto un 4% annuo.
Ciò costringerebbe il nostro investitore originario(…il contadino insomma), se vuole rivendere almeno a 100, ad aspettare la scadenza del titolo.
Più lontana è la scadenza, più c’è da aspettare.
Si definisce quindi rendimento EFFETTIVO quello che il risparmiatore ottiene REALMENTE comprando un titolo ad una certa data, riscuotendo le cedole e tenendolo fino a scadenza.
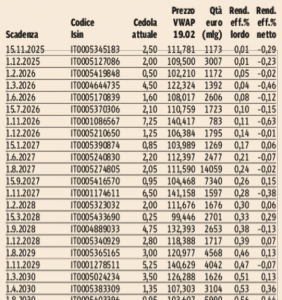
Se mi compro un BTP scadenza 1/3/2030, ad esempio, prendo fino ad allora delle cedole del 3,5% annue, ma lo pago 126,28 e il suo valore si andrà gradualmente ad avvicinare a 100 fino al marzo del 2030, quando lo Stato lo rimborserà, appunto a prezzo 100.
Quindi a 100 devo aggiungere 3,5 per 10 volte, ma sottrarre 26,28, che è il prezzo che pago in più per averlo ora.
Il calcolo preciso si trova sul Sole24ore tutti i giorni.
Nel mio caso, al netto delle tasse e reinvestendo nello stesso titolo le cedole (mai visto in 26 anni!), si avrebbe un rendimento annuo dello 0,13 %. Tutto chiaro?
Morale?
In questo momento i tassi di interesse di mercato sono bassissimi (talora perfino negativi), infatti ad esempio moltissimi BTP quotano sul mercato ben sopra il 100, come si è visto.
Chi avesse acquistato di recente titoli di stato a lungo termine rischia di dover aspettare parecchio prima di vedere un minimo di rendimento e/o il proprio capitale intatto.
E chi è che acquista titoli di debito a lungo termine(diciamo sopra i 10 anni di durata)? Molti risparmiatori impauriti dal “rischio”, ad esempio. Pressoché tutte le assicurazioni, per investire i soldi dei risparmiatori che sono impauriti dal “rischio”, ecc…
Sicuri di non avere titoli di stato a lungo termine in portafoglio? Magari mascherati da polizze di vario genere?
Meditate gente, meditate…
